The formula cos 2A = cos2 A − sin which is yet a third form 27 Related Question Answers Found How do you integrate Cos 2x?Question Find all solutions of sec^2xtan^2x=3 in the interval 0,2pi Found 2 solutions by Alan3354, stanbon Answer by Alan3354() ( Show Source )=> `tan x*cot x tan^2x` => `1 tan^2x` => `1 (sin^2x)/(cos^2x)` => `(cos^2x sin^2x)/(cos^2x)` =` `> `1/(cos^2x)` => `sec^2x` This proves that `tan x(cot x tan x) = sec^2 x`
1
Sec^2x=1+tan^2x proof
Sec^2x=1+tan^2x proof- Ex 34, 8 Find the general solution of the equation sec2 2x = 1 – tan 2x sec2 2x = 1 – tan 2x 1 tan2 2x = 1 – tan2x tan2 2x tan2x = 1 – 1 tan2 2x tan2x = 0 tan 2x (tan2x 1) = 0 Hence We know that sec2 x = 1 tan2 x So, sec2 2x = 1 tan2 2x tan 2x = 0 tan 2x 1 = 0 tan 2x = –1 We find general solutions for both separately General solution for tan 2x = 0 Let tan x = tan yAnswer by Fermat (136) ( Show Source ) You can put this solution on YOUR website!




4 Tan 2x 2 Sec 2x 1 0 X In 0
cos2x=(1tan^2x)/(1tan^2x) =(1tan^2x)/sec^2x =(1tan^2x)cos^x =cos^xsin^x =cos2x5 tan^2x sec^2x = 1 we can convert this into tan^2x=sec^2x1 if tan^2x1=sec^2x then tan^2x=sec^2x1 so both sides are equal Share this link with a friend Copied! One answer is to say that, properly, the identity is $\sec^2x=1\tan^2x$, where the sides fail to be defined at the same values Share Improve this answer Follow edited Nov 27 '15 at 2246 Joel Reyes Noche $\begingroup$ I don't think the OP really wants a proof of the identity The problem seems to be about making sense of it or
Math Tutor or Teacher amanpreetjaggi, replied 10 years ago amanpreetjaggi Category Math Homework Satisfied Customers740 Verified Hi,Welcome to JustAnswer (1tan^2x)/(1cot^2x) = 1sec^2x Substitutetan x = sinx/cosx and cot x = cosx/sinx in the left hand part of the equation(1tan^2x)/(1cot^2x) = 1 (sinx/cosx)^2/ 1 (cosx/sinx)^2= (cos^x So the equation (i) after substituting becomes tan 2 (x) 1= 1/cos 2 (x) ——– (ii) Now we know that 1/cos 2 (x)= sec 2 (x) So on substitution equation (ii) becomes tan 2 (x) 1= sec 2 (x) On rearranging the terms we get sec 2 x−1=tan 2 x Hence ProvedStudents who viewed this also studied University of Wisconsin, Eau Claire
Yes, sec2−1=tan2x is an identity Prove that the equation Is an identity Sec^4x Tan^4x = Sec^2x Tan^2x Math What is a simplified form of the expression sec^2x1/sin x sec x ?1 tan^2x 1 (sin^2x/cos^2x) (cos^2x sin^2x)/cos^2x (12sin^2x)sec^2x (12sin^2x) (1tan^2x)




Iit 1994 Prove That Sec2x Tan2x Tan Pi 4 X When X Lies Between 0 And Pi 4 Youtube




Inquiry 11 8 Marks Prove The Following Trig Chegg Com
In this video, I go through a trigonometric proof which is1tan^2=sec^2The proof is fairly straight forward with some common knowledge of trigonometric fuTan^2x sec^2x = 1, Answers Answer from burners Hey there ) tan²x sec²x = 1 or 1 tan²x = sec²x sin²x cos²x = 1 Divide the whole by cos²xSec^6xtan^6x = 1 3 (tan^2x) (sec^2x) Lilp22 View Public Profile Find latest posts by Lilp22 neerajtiwari Posts 2, Reputation 1 New Member , 1053 PM Left Hand Side = sec^6 x tan^6 x = (sec²x tan²x) (sec^4 x (tan²x) (sec²x) tan^4 x)



Http Www Whsd K12 Pa Us Userfiles 1598 Classes 9713 Trig chapter 5 notes Pdf



2
Prove this trigonometric equation; Proof Recall from the last section, the sine of the sum of two angles sin(α β) = sin α cos β cos α sin β We will use this to obtain the sine of a double angle If we take the left hand side (LHS) sin(α β) and replace β with α, we get sin(α β) = sin(α α) = sin 2α Consider the RHS sin α cos β cos α sin βTanx = t Sec^2 x dx= dt So now it is, 1/ (1t)^2 dt This integral is given by 1/1t and t= tanx So, it is cosx/cosx sinx tanx = t Sec^2 x dx= dt So now it is, 1/ (1t)^2 dt This integral is given by 1/1t and t= tanx So, it is cosx/cosx sinx Integral of the function \frac {\cos ^2 x} {1\tan x}




Ppt Using Basic Trick For Trigonometric Functions Fullmakrseducare Powerpoint Presentation Id



1
1tan^2x=sec^2x Change to sines and cosines then simplify 1tan^2x=1(sin^2x)/cos^2x =(cos^2xsin^2x)/cos^2x but cos^2xsin^2x=1 we have1tan^2x=1/cos^2x=sec^2x Trigonometry Science The correct identities are 1 tan^2x = sec^2x 1 cot^2x = csc^2x sin^2x cos^2x = 1 which correspond to B and D thank you!!!Tanx = t Sec^2 x dx= dt So now it is, 1/ (1t)^2 dt This integral👍 Correct answer to the question Prove that tan^2x sec^2x=1 eeduanswerscomMathematics, 0330 momo842 Which expression is equivalent to sec^2xcot^2x?




New Syllabus Additional Mathematics Pages 301 350 Flip Pdf Download Fliphtml5




How Do You Simplify Sec 4x Tan 4x Sec 2x Tan 2x Socratic
Let me tell you first, you can type roof of sign by pressing (left) Alt 251 ( √ ) and pi sign by prssing (left) Alt 227 ( π ) We have, cot x = √3 or, tan x = 1/√3 = tan (π/6) or, x = nπ ( π/6 ), where n belongs to the set of integers Hence, the general solution is x = nπ (π/6), where n belongs to the set of integersGet stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!Is SEC 2x 1 tan 2x an identity?



Q Tbn And9gcsxz Hkczzvj4wy3gx0dbnqphk3hi Cp Rmi Vgbp2veivzqwuc Usqp Cau
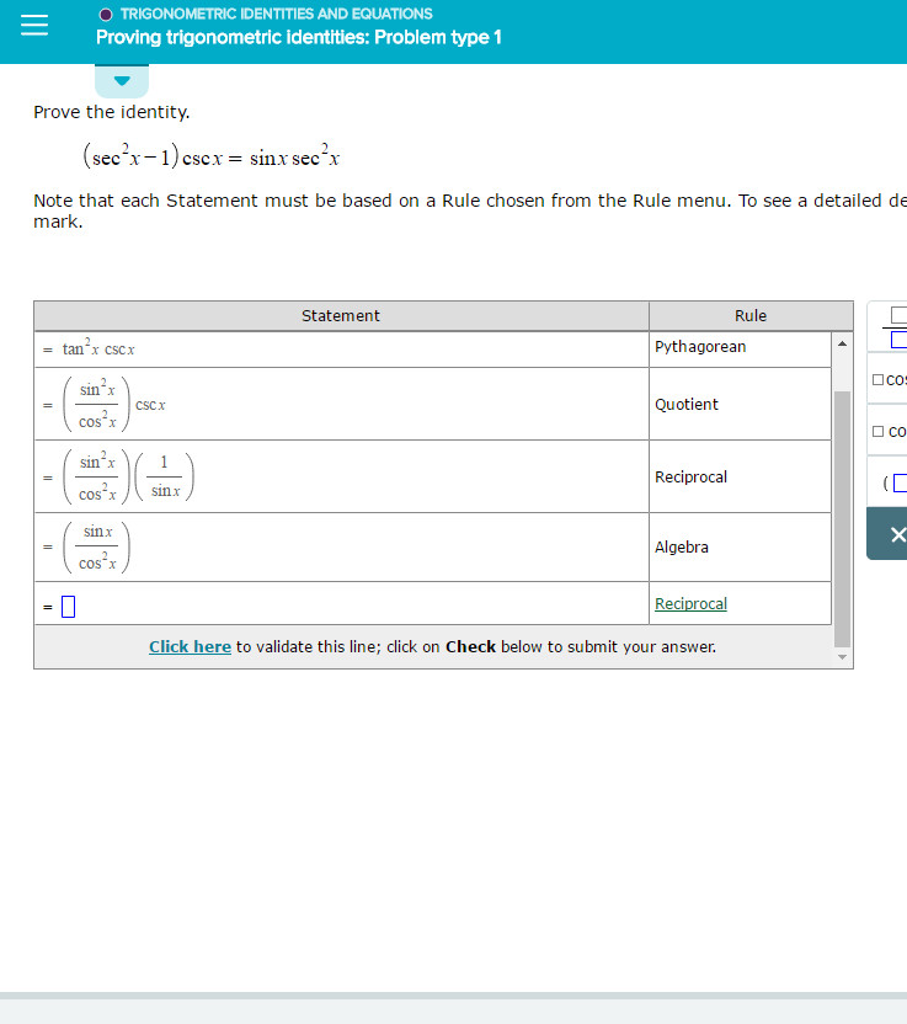



Prove The Identity Sec 2x 1 Csc X Sin X Sec 2 X Chegg Com
To prove this you will need to know a bit of algebra namely that x³ y³ = (x – y)(x² xy y²) and a variety of trig identities namely tan x = sinx/cosx, cot x = cos x/sinx, sin² x cos² x = 1Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more It's a simple proof, really What is the formula for cos 2a?




Integral Of Cos 2x Tan 4x




If Tan 2 X Sec X A 0 Has Atleast One Solution Then Complete Set Of V Askiitians
Now sec^2x = 1tan^2x and manipulating does indeed yield the identity ) 0 reply nota bene Badges 15 Rep?`= 12tanxtan^2x12cotxcot^2x` (1cot^2x)2(tanxcotx)` We know that;Free trigonometric identities list trigonometric identities by request stepbystep



2



1
A)cot x b)csc x c)tan x d)sec x tan x Please help me ( Math Trig 1 Determine the exact value of cos^1Integration of tan^2x sec^2x/ 1tan^6x dx Ask questions, doubts, problems and we will help youTan^2xsec^2x/1tan^6x Ask questions, doubts, problems and we will help you




Trig Identities Worksheet With Answers 2




Sinx Cosx Sinx Cos X Sec 2 X 2 Tan 2 X 1 Where X In 0 Pi 2
Trig Use the fundamental identities to simplify the expression cot beta sec beta I used 1tan^2u=secu since cot is the inverse of tan I flipped the tangent, then so it was 1 (1/tan)Proving Trigonometric Identities Calculator Get detailed solutions to your math problems with our Proving Trigonometric Identities stepbystep calculator Practice your math skills and learn step by step with our math solver Check out all of our online calculators here!Complete the proof of the identity by choosing the Rule that justifies each step cosx (1 tan 2x)secr To see a detailed description of a Rule in the Rule menu, select the corresponding question marProve the identity (1tanx) cotx=secx csex Note that each Statement must be based on a Rule chosen from the Rule menu




Prove That Tex Frac Sin 2x Sec X 1 Frac Sec 2x Sec 2x 1 Tan Frac X 2 Tex Brainly In




Prove That Sec8x 1 Sec4x 1 Tan8x Tan2x
I know that and The next step would then be to say that but now what?Separate fractions Rewrite tan(x) tan ( x) in terms of sines and cosines Multiply by the reciprocal of the fraction to divide by sin(x) cos(x) sin ( x) cos ( x) Convert from cos(x) sin(x) cos ( x) sin ( x) to cot(x) cot ( x) Divide sec2(x) sec 2 ( x) by 1 1 Rewrite sec(x) sec ( x) in terms of sines and cosines Tan^2 x1=sec^2x So to get 1 on the other side of the equal sign wouldn't it be sec^2xtan^2x=1?Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!1 A water molecule is held together by two single polar covalent bonds False 2 Because oxygen has a greater electronegativity than hydrogen, water molecules are polar with




How Many Can You Derive From First Principles Ppt Download




Sec 2 2x 1 Tan2x Youtube
The cos2(2x) term is another trigonometric integral with an even power, requiring the powerreducing formula again The cos3(2x) term is a cosine function with an odd power, requiring a substitution as done before We integrate each in turn below ∫cos2(2x) dx = ∫ 1 cos(4x) 2 dx = 1 2 (x 1 4sin(4x)) C Sec^2x=1tan^2x proof Sec^2x=1tan^2x proofD is the differential operator, int is the integration operator, C is the constant of integration Identities tan x = sin x/cos x equation 1 cot x = cos x/sin x equation 2 sec x = 1/cos x equation 3 csc x = 1/sin x equation 4Verify the identity {eq}\sec^4x \sec^2x = \tan^4x \tan^2x {/eq} Verifying a Trigonometric Equation Suppose we are Starting from cos2(x) sin2(x) = 1 Divide both sides by cos2(x) to get cos2(x) cos2(x) sin2(x) cos2(x) = 1 cos2(x) which simplifies to 1 tan2(x) = sec2(x) Answer link




Tan4x Tanx Sec4x 1 Sec2x 1 Brainly In




Prove Identity Tan 3x 1 Tanx 1 Sec 2x Tanx Brainly In
Trigonometric Identities Solver \square!Proving $(\sec^2x\tan^2x)(\csc^2x\cot^2x)=12\sec^2x\csc^2x$ and $\frac{\cos x}{1\tan x}\frac{\sin x}{1\cot x} = \sin x \cos x $ 0 How to find the least value of $\cot x \frac{\csc^2x\cot ^4x}{\csc^2x\cot x}\tan x \frac{\sec^2x\tan^4x}{\sec^2x\tan x}$?Proportionality constants are written within the image sin θ, cos θ, tan θ, where θ is the common measure of five acute angles In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a rightangled triangle to ratios of two side lengths



Pmt Physicsandmathstutor Com Download Maths A Level C3 Topic Qs Edexcel Set 1 C3 trigonometry trigonometric identities Pdf



Www Birmingham K12 Mi Us Cms Lib Mi Centricity Domain 976 Chapter 5 Pdf
You could take tan(x) out of the fraction, but I still don't know how to go about simplifying it The book says the answer isThe angle sum tan identity is a trigonometric identity, used as a formula to expanded tangent of sum of two angles For example, $\tan{(AB)}$, $\tan{(xy)}$, $\tan{(\alpha\beta)}$, and so on You know the tan of sum of two angles formula but it is very important for you to know how the angle sum identity is derived in mathematics1 cos ( x) − cos ( x) 1 sin ( x) = tan ( x) Go!



2




The Derivative Of Tan X Is Sec 2 X Why Mathematics Stack Exchange
Verify the Identity cot (x)^2 (sec (x)^21)=1 cot2 (x) (sec2 (x) − 1) = 1 cot 2 ( x) ( sec 2 ( x) 1) = 1 Start on the left side cot2(x)(sec2(x)−1) cot 2 ( x) ( sec 2 ( x) 1) Apply pythagorean identity cot2(x)tan2(x) cot 2 ( x) tan 2 ( x) Convert to sines and cosines Tap for more steps Write cot ( x) cot ( x) in sines and cosines\begin{align} 1^2 tan^2x = sec^2x \quad 1^2 cot^2x = csc^2x \end{align} Proof of Pythagorean Trigonometric Identity Equivalencies We will not prove the unit circle trigonometric identity because it is already geometrically proven on the unit circle page`1tan^2x = sec^2x` `1cot^2x = cosec^2x` `sin^2xcos^2x = 1` `(tanxcotx)` `= sinx/cosxcosx/sinx` So the proof
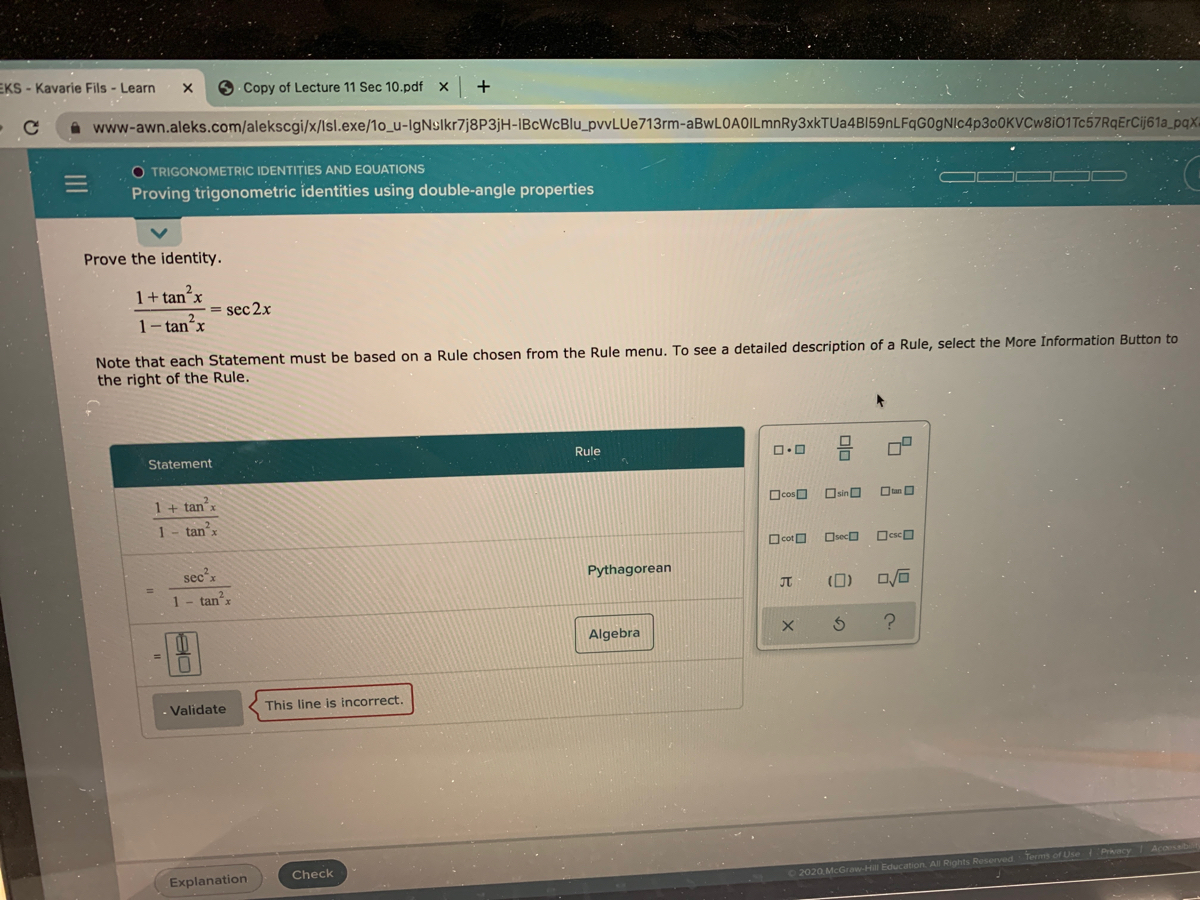



Answered Prove The Identity 1 Tanx Sec 2x 2 1 Bartleby




Trigonometric Identities Questions And Answers Topperlearning
#4 Report 14 years ago #4 (Original post by chrisjorg) I got it now, the trick is to make 1/cos^2x = sec^2x Now sec^2x = 1tan^2x and manipulating does indeed yield the identity Prove the following identities $$(\sec^2 x \tan^2x)(\csc^2 x \cot^2x) = 1 2 \sec^2x \csc^2 x \tag i$$ $$\frac{\cos x}{1\tan x} \frac{\sin x}{1\cot x} = \sin x \cos x \tag {ii}$$ For $(\mathrm i)$ , I initially tried simplifying what was in the 2 brackets but ended up getting 1 1




Use A Similar Line Of Reasoning To Prove That 1 T Gauthmath




Ma 18 Lt 5 Ams Lt Archives




Prove That Tan 45 X Sec2x Tan2x




Prove The Following Identities I 4 Marks Each A Gauthmath




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo




Every Day I M Calculatin I D3 Unit Q Pythagorean Identities




Trigonometry Identity Tan 2 X 1 Sec 2 X Youtube




Misc 38 Prove That 2 Tan3 X Dx 1 Log2 Cbse Miscellaneous



Www Southhadleyschools Org Cms Lib Ma Centricity Domain 11 5 6 Pdf




Tan2x Sec2x ただの悪魔の画像




Proof That The Derivative Of Tan X Sec 2x Using The Quotient Rule Album On Imgur




Inverse Trigonometric Functions General Solution Of




Tan2x ただの悪魔の画像




How Do You Prove The Identity Tan 2x Secx 1 1 Cosx Cosx Socratic



Trigonometry Functions User S Blog




Cos2xu003dcosx
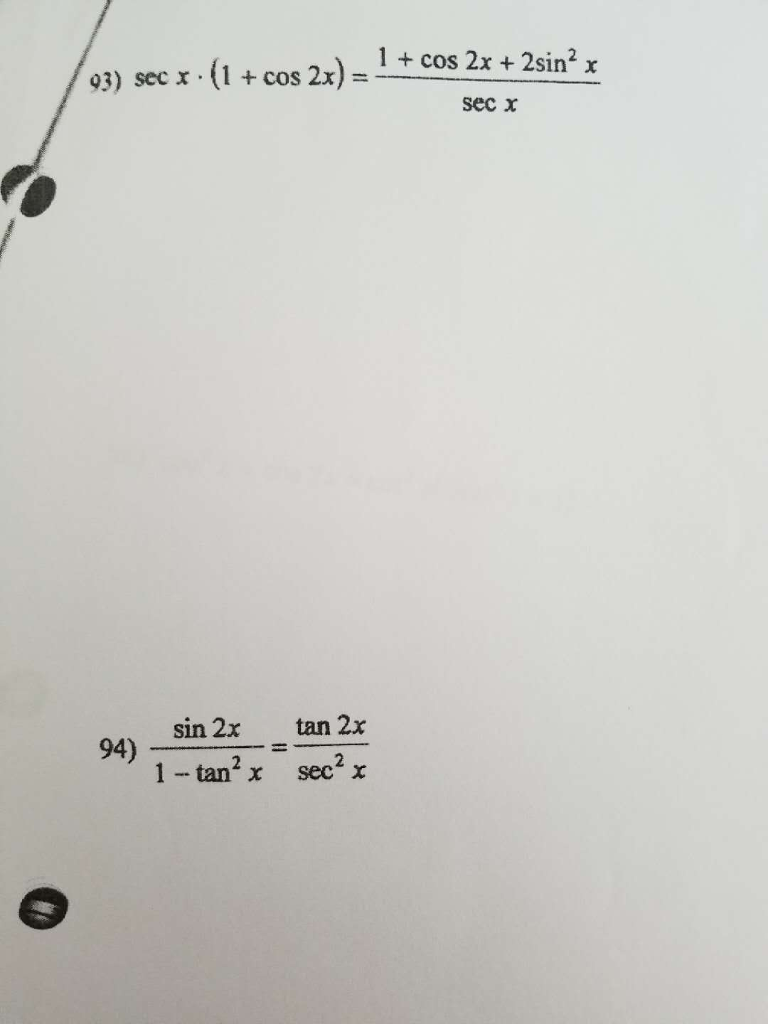



Solved Verify Each Identity Solve As A Two Column Proof Chegg Com




Tan 2x Tan 2x




Sec 6x Tan 6x 1 2 Tan 2x Sec 2x Important Difficult Trigonometric Identity Youtube




Limit Trigonometric Function 2 Sec 2x 1 Tan X Youtube




How Many Can You Derive From First Principles Ppt Download




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo




1 Tan 2x 1 Cos 2x Sin 2x 2sin 4x 1 Sin 2x Trigonometric Identities Mcr3u Youtube



3




Prove The Identity 11 Frac 1 2 Sin X 3sec 2 X Tan Gauthmath




Exercise 7 3 Integrals Of The Functions In Exercises 1 To 22 2 Sin 3x Cos 4x 3 Cos 2x Cos 4x Cos 6x 5 Sin X Cos 6 Sin X Sin 2x




1 Tan1 1 Tan2 1 Tan3 1 Tan45 2 N Brainly In Ryad Antonio Ebooks En Ligne Gratuit



Solved Prove The Following Trig Identity Sec 2 X 2secx Cosx Cos 2 X Tan 2 X Sin 2 X Course Hero




Rd Sharma Solutions For Class 10 Chapter 6 Trigonometric Identities Exercise 6 1 Get Pdf



How To Show That Sec X Tan X 1 Sec X Tan X Quora



Tan 2x Tan 2x




Cos2xu003dcosx




C3 Chapters 6 7 Trigonometry Ppt Download




How Do You Verify 4tan 4 Tan 2x 3 Sec 2x 4tan 2x 3 Kinda Hard Please With All The Steps Thanks Socratic




Ex 3 3 23 Prove Tan 4x 4 Tan X 1 Tan2 X 1 6tan2x




How Do You Prove The Identities Cosx Secx Sinx Cscx Sec 2x Tan 2x Socratic



Solved Prove The Following Trig Identities Course Hero




Basictrigonometry Pdf Trigonometric Functions Sine
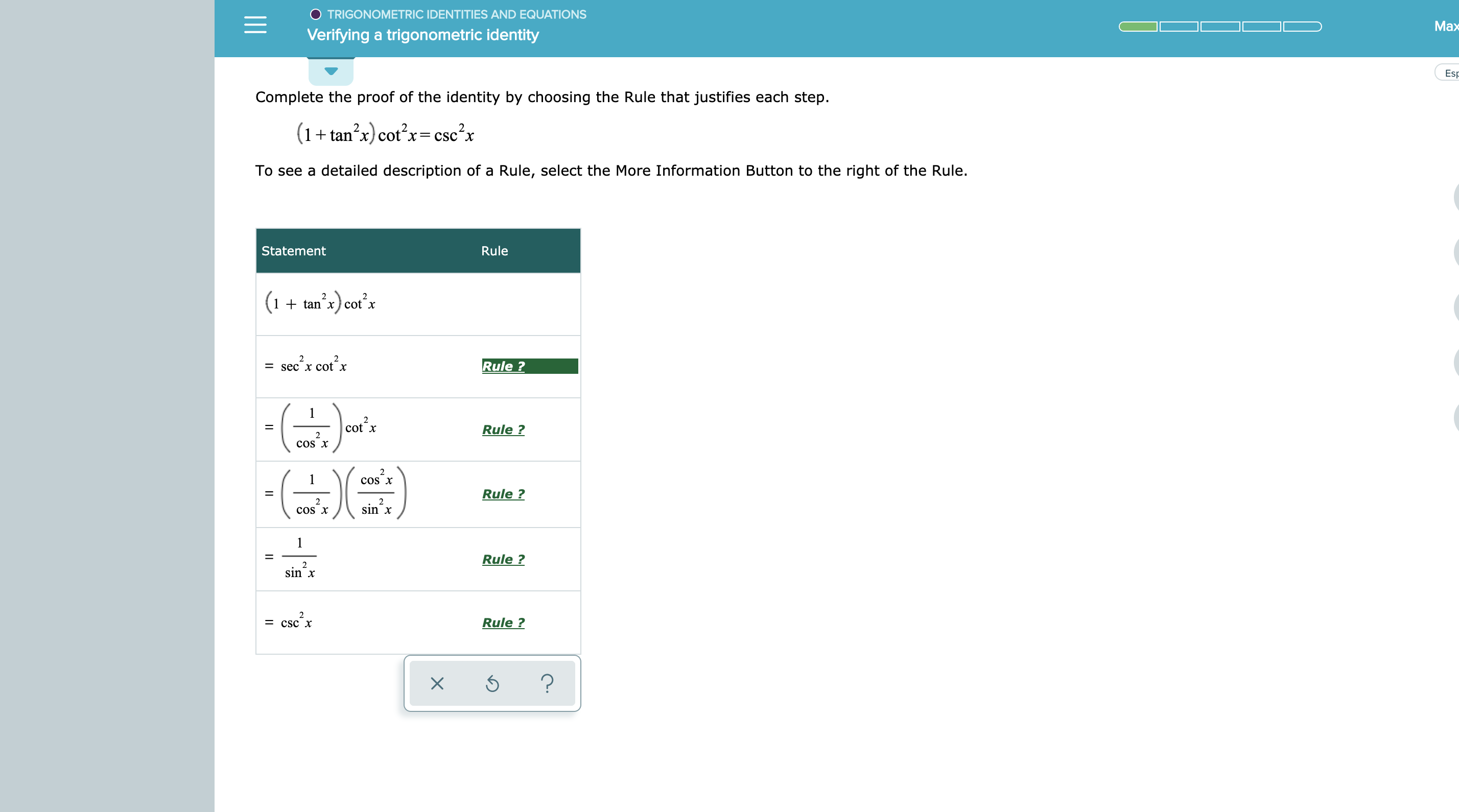



Answered Trigonometric Identities And Equations Bartleby




If F 2tanx 1 Tan 2x Cos2x 1 Sec 2x Tanx 2 Then F X




Trigonometric Identity In Double Angle Sin2x Cos2x 1 Sin2x Cos2x 1 Sec2x Tan2x Youtube




4 Tan 2x 2 Sec 2x 1 0 X In 0




Let Tan 2x 1 2tan 2 Y Then Prove That Cos 2y 1 2cos 2x



2



Www2 Math Binghamton Edu Lib Exe Fetch Php People Mckenzie Trig Identities Worksheet With Answers 2 Pdf
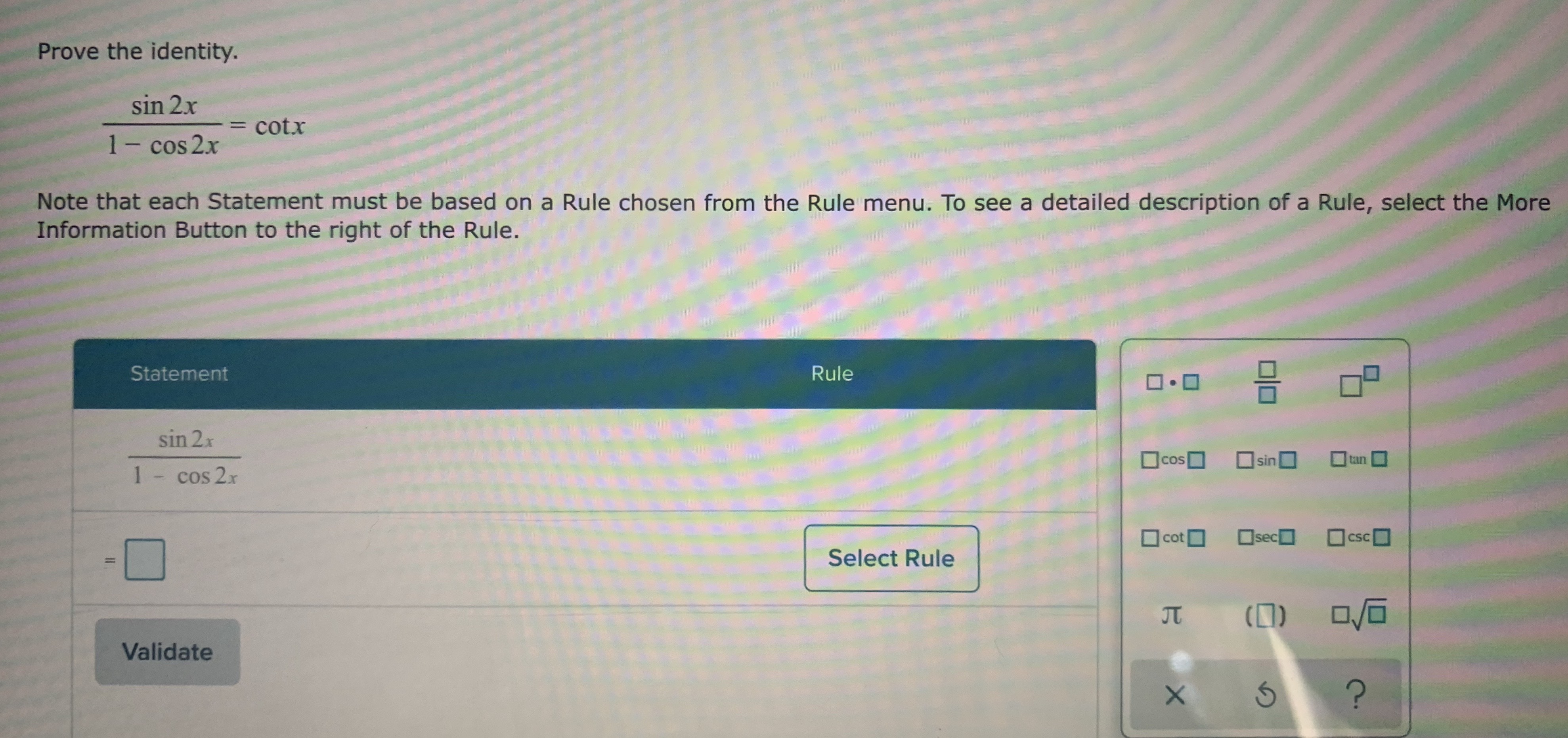



Answered Prove The Identity Sin 2x Cotx 3d 1 Bartleby



Www2 Math Binghamton Edu Lib Exe Fetch Php People Mckenzie Trig Identities Worksheet With Answers 2 Pdf
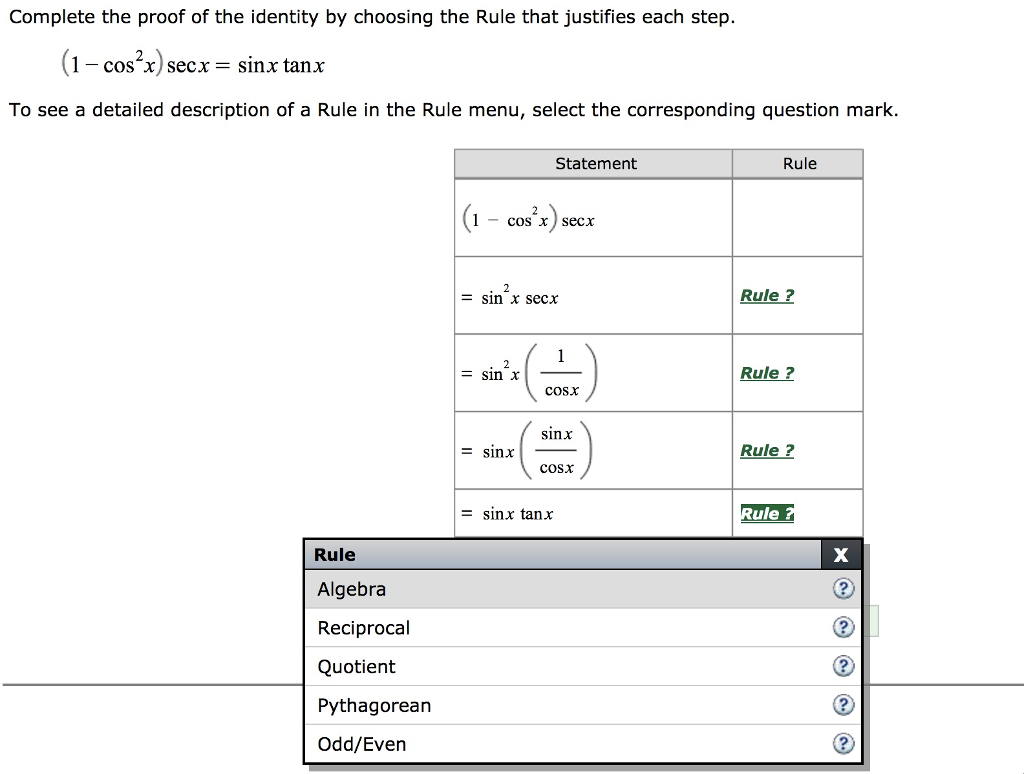



Complete The Proof Of The Identity By Choosing The Chegg Com




Prove That Sec 6x Tan 6 X 1 3sec 2x Tan 2x Brainly In



2




3 09 Trigonometry Trigonometric Functions Trigonometry



Solved Prove The Following Trigonometric Identity Tan 2x Tan X Sec 2x 1 For Each Step Of Your Proof Include A Written Rationale And Or Indi Course Hero




How Many Can You Derive From First Principles Ppt Download



Prove That Frac Tan Theta 1 Cot Theta Frac Cot Theta 1 Tan Theta 1 Mathit Sec Theta Cosectheta Orif Mathit Sec Theta X Frac 1 4x Then Prove That Mathit Sec Theta Tan Theta 2x Or Frac 1 2x Snapsolve




Ppt Analytic Trig Powerpoint Presentation Free Download Id




Trig Identity Sec2x Minus Tan2x T10 Youtube



How Do You Verify Cot 2x Sec 2x Csc 2x Socratic
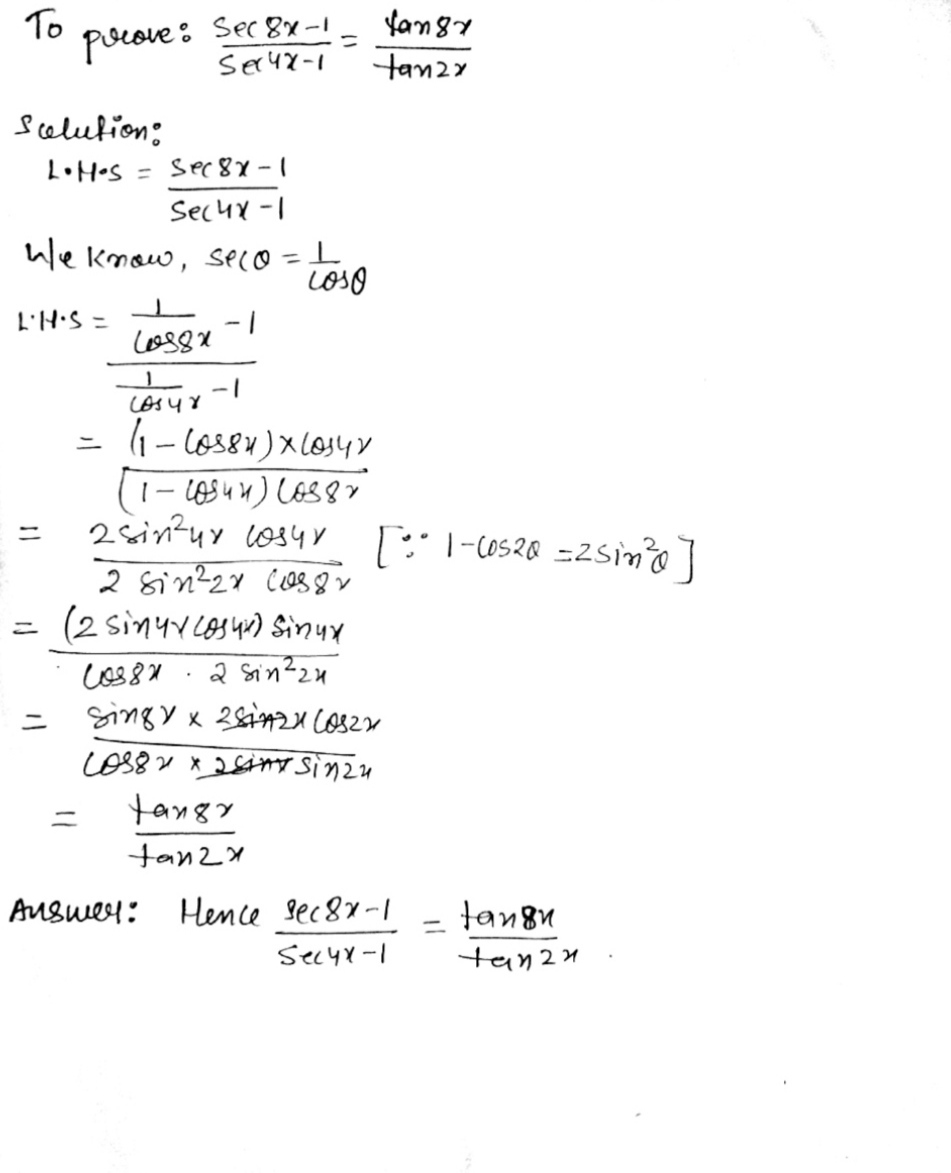



Prove That Frac Mathit Sec 8x 1 Mathit Sec 4x 1 Frac Tan 8x Tan 2x Snapsolve




Solution If Sec 2x 3 1 Sin 5x 9 Determine X In Degrees



2




Sin2x Cos2x 1 Proof




Www Mercadocapital Sec 2x 2 Tan 2x Trigonometric Identities




Rd Sharma Solutions For Class 11 Chapter 5 Trigonometric Functions



Www Jensenmath Ca Unit 5 pretest review solutions Pdf




How Do You Prove Tan 2x Secx 1 1 Secx Socratic




5 Pts Each Prove Tan 8 Sin 2 8 2sin 2 8 Gauthmath




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo



How To Prove D Dx Tanx Sec 2x Without Using Tanx Sinx Cosx And Instead Use Tan X H Tanx Tanh 1 Tanxtanh Quora




Derivative Of Tan X Old Video Khan Academy




How Do You Prove Tan 2x Secx 1 1 Secx Socratic




Sec 2 X Cosec 2x Tan X Cot X Prove It Brainly In




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo




The Derivative Of Tan X Is Sec 2 X Why Mathematics Stack Exchange




Prove That Tan 2 2x Tan 2 X1 Tan 2 2x Tan 2 X Tan 3x Tan X



Http Theprofessorshut Weebly Com Uploads 2 3 2 7 Pc Chap 6 Sect 2 Sum Difference And Cofunction Identities Pdf



Qcweb Qc Edu Hk Math Small problems Harder trigonometry problems Pdf



No comments:
Post a Comment